
Journal of Geodesy and Geoinformation Science ›› 2023, Vol. 6 ›› Issue (3): 76-86.doi: 10.11947/j.JGGS.2023.0308
• Literature Review • Previous Articles Next Articles
Tao JIANG1( ), Xinyu XU2(
), Xinyu XU2( ), Yonghai CHU2, Taoyong JIN2,3, Wei LIANG4, Yihao WU5, Yanguang FU6, Yongqi ZHAO2, Xinwei GUO7
), Yonghai CHU2, Taoyong JIN2,3, Wei LIANG4, Yihao WU5, Yanguang FU6, Yongqi ZHAO2, Xinwei GUO7
Received:2023-08-22
Accepted:2023-08-26
Online:2023-09-20
Published:2023-10-31
Contact:
Xinyu XU E-mail: About author:Tao JIANG (1984—), male, PhD, professor, majors in Earth gravity field and vertical datum. E-mail: jiangtao@casm.ac.cn
Supported by:Tao JIANG, Xinyu XU, Yonghai CHU, Taoyong JIN, Wei LIANG, Yihao WU, Yanguang FU, Yongqi ZHAO, Xinwei GUO. Review of the Research Progress on Static Earth Gravity Field and Vertical Datum in China during 2019—2023[J]. Journal of Geodesy and Geoinformation Science, 2023, 6(3): 76-86.
Add to citation manager EndNote|Reference Manager|ProCite|BibTeX|RefWorks
Tab.1
Statistical results of GOCE-related models compared with GNSS leveling data in the USA (6169 points) and mainland China (649 points)m"
| Model | Max | Min | Mean | STD | |
|---|---|---|---|---|---|
| USA | GOSG02S | 1.046 | -2.184 | -0.562 | 0.441 |
| WHU-SWPU-GOGR2022S | 1.050 | -2.179 | -0.561 | 0.440 | |
| GO_CONS_GCF_2_DIR_R6 | 1.080 | -2.196 | -0.565 | 0.438 | |
| GO_CONS_GCF_2_TIM_R6 | 1.038 | -2.221 | -0.554 | 0.432 | |
| Tongji-GMMG2021S | 1.068 | -2.193 | -0.561 | 0.437 | |
| GOCO06s | 1.001 | -2.234 | -0.557 | 0.435 | |
| China | GOSG02S | 1.023 | -1.690 | 0.073 | 0.388 |
| WHU-SWPU-GOGR2022S | 1.024 | -1.689 | 0.070 | 0.389 | |
| GO_CONS_GCF_2_DIR_R6 | 0.969 | -1.640 | 0.070 | 0.391 | |
| GO_CONS_GCF_2_TIM_R6 | 0.963 | -1.584 | 0.075 | 0.385 | |
| Tongji-GMMG2021S | 1.070 | -1.665 | 0.072 | 0.389 | |
| GOCO06s | 0.953 | -1.578 | 0.072 | 0.384 |
Tab.2
Statistical results of comparison with GNSS leveling data in the USA (6169 points) and mainland China (649 points)m"
| Model | Max | Min | Mean | STD | RMS | |
|---|---|---|---|---|---|---|
| USA | EGM2008 | 0.360 | -1.396 | -0.511 | 0.284 | 0.584 |
| SGG-UGM-1 | 0.317 | -1.407 | -0.511 | 0.280 | 0.583 | |
| SGG-UGM-2 | 0.386 | -1.394 | -0.511 | 0.277 | 0.578 | |
| GECO | 0.313 | -1.391 | -0.513 | 0.281 | 0.585 | |
| EIGEN-6C4 | 0.397 | -1.392 | -0.512 | 0.282 | 0.585 | |
| XGM2019e_2159 | 0.345 | -1.404 | -0.507 | 0.277 | 0.578 | |
| China | EGM2008 | 1.729 | -1.535 | 0.239 | 0.240 | 0.339 |
| SGG-UGM-1 | 0.744 | -0.618 | 0.246 | 0.162 | 0.294 | |
| SGG-UGM-2 | 0.744 | -0.603 | 0.246 | 0.161 | 0.292 | |
| GECO | 1.165 | -0.847 | 0.244 | 0.180 | 0.303 | |
| EIGEN-6C4 | 0.729 | -0.698 | 0.243 | 0.157 | 0.289 | |
| XGM2019e_2159 | 0.630 | -0.761 | 0.244 | 0.143 | 0.283 |
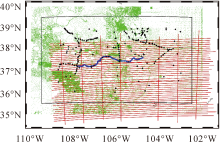
Fig.2
Distribution of terrestrial, airborne gravity and historic GNSS leveling and GSVS17 GNSS leveling data in Colorado (Green points represent terrestrial gravity observations; red lines represent GRAV-D airborne gravity data; black diamonds represent historic GNSS leveling benchmarks; bule points stand for GSVS17 GNSS leveling benchmarks; and the geoid computation area is bounded by the black rectangular)"
| [1] | CHEN Jianhua, ZHANG Xingfu, CHEN Qiujie, et al. Static gravity field recovery and accuracy analysis based on reprocessed GOCE level 1b gravity gradient observations[C]// Proceedings of EGU General Assembly 2022. Vienna, Austria: EGU, 2022. |
| [2] | ZHAO Yongqi, LI Jiancheng, XU Xinyu, et al. Determination of static gravity field model by using satellite data of GOCE and GRACE[J]. Chinese Journal of Geophysics, 2023, 66(6): 2322-2336. |
| [3] |
CHEN Qiujie, SHEN Yunzhong, FRANCIS O, et al. Tongji-Grace02s and Tongji-Grace02k: high-precision static GRACE-only global earth’s gravity field models derived by refined data processing strategies[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(7): 6111-6137.
doi: 10.1029/2018JB015641 |
| [4] |
Liang Wei, Li Jiancheng, Xu Xinyu, et al. A high-resolution earth’s gravity field model SGG-UGM-2 from GOCE, GRACE, satellite altimetry, and EGM2008[J]. Engineering, 2020, 6(8): 860-878.
doi: 10.1016/j.eng.2020.05.008 |
| [5] |
JEAN Y, MEYER U, JÄGGI A. Combination of GRACE monthly gravity field solutions from different processing strategies[J]. Journal of Geodesy, 2018, 92(11): 1313-1328.
doi: 10.1007/s00190-018-1123-5 |
| [6] |
KOCH K R, KUSCHE J. Regularization of geopotential determination from satellite data by variance components[J]. Journal of Geodesy, 2002, 76(5): 259-268.
doi: 10.1007/s00190-002-0245-x |
| [7] |
ZINGERLE P, PAIL R, GRUBER T, et al. The combined global gravity field model XGM2019e[J]. Journal of Geodesy, 2020, 94(7): 66.
doi: 10.1007/s00190-020-01398-0 |
| [8] |
JIANG Tao, DANG Yamin, ZHANG Chuanyin. Gravimetric geoid modeling from the combination of satellite gravity model, terrestrial and airborne gravity data: a case study in the mountainous area, Colorado[J]. Earth, Planets and Space, 2020, 72(1): 189.
doi: 10.1186/s40623-020-01287-y |
| [9] |
WU Yihao, ABULAITIJIANG A, FEATHERSTONE W E, et al. Coastal gravity field refinement by combining airborne and ground-based data[J]. Journal of Geodesy, 2019, 93(12): 2569-2584.
doi: 10.1007/s00190-019-01320-3 |
| [10] | SJÖBERG L E. Comparison of some methods of modifying Stokes’ formula[J]. Bollettino di Geodesia e Scienze Affini, 1986, 45(3): 229-248. |
| [11] | ÅGREN J. Regional geoid determination methods for the era of satellite gravimetry[D]. Stockholm, Sweden: Royal Institute of Technology, 2004. |
| [12] |
JIANG Tao, WANG Yanming. On the spectral combination of satellite gravity model, terrestrial and airborne gravity data for local gravimetric geoid computation[J]. Journal of Geodesy, 2016, 90(12): 1405-1418.
doi: 10.1007/s00190-016-0932-7 |
| [13] |
JIANG Tao. On the contribution of airborne gravity data to gravimetric quasigeoid modelling: a case study over Mu Us area, China[J]. Geophysical Journal International, 2018, 215(2): 1308-1321.
doi: 10.1093/gji/ggy346 |
| [14] |
WANG Yanming, SÁNCHEZ L, ÅGREN J, et al. Colorado geoid computation experiment: overview and summary[J]. Journal of Geodesy, 2021, 95(12): 127.
doi: 10.1007/s00190-021-01567-9 |
| [15] | FORSBERG R. A new covariance model for inertial gravimetry and gradiometry[J]. Journal of Geophysical Research: Solid Earth, 1987, 92(B2): 1305-1310. |
| [16] | FORSBERG R. Downward continuation of airborne gravity—an Arctic case story[C]// Proceedings of International Gravity and Geoid Commission Meeting. Thessaloniki,Greece:[s.n.], 2002. |
| [17] |
KLEES R, TENZER R, PRUTKIN I, et al. A data-driven approach to local gravity field modelling using spherical radial basis functions[J]. Journal of Geodesy, 2008, 82(8): 457-471.
doi: 10.1007/s00190-007-0196-3 |
| [18] |
WU Yihao, ZHOU Hao, ZHONG Bo, et al. Regional gravity field recovery using the GOCE gravity gradient tensor and heterogeneous gravimetry and altimetry data[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(8): 6928-6952.
doi: 10.1002/jgrb.v122.8 |
| [19] |
FLURY J, RUMMEL R. On the geoid-quasigeoid separation in mountain areas[J]. Journal of Geodesy, 2009, 83(9): 829-847.
doi: 10.1007/s00190-009-0302-9 |
| [20] |
FLURY J, RUMMEL R. On the computation of the geoid-quasigeoid separation[J]. Journal of Geodesy, 2011, 85(3): 185-186.
doi: 10.1007/s00190-011-0447-1 |
| [21] |
SJÖBERG L E. A strict formula for geoid-to-quasigeoid separation[J]. Journal of Geodesy, 2010, 84(11): 699-702.
doi: 10.1007/s00190-010-0407-1 |
| [22] |
WANG Yanming, VÉRONNEAU M, HUANG Jianliang, et al. Accurate computation of geoid-quasigeoid separation in mountainous region—a case study in Colorado with full extension to the experimental geoid region[J]. Journal of Geodetic Science, 2023, 13(1): 20220128.
doi: 10.1515/jogs-2022-0128 |
| [23] | DANG Yamin, GUO Chunxi, JIANG Tao, et al. 2020 height measurement and determination of Mount Qomolangma[J]. Acta Geodaetica et Cartographica Sinica, 2021, 50(4): 556-561. DOI: 10.11947/j.AGCS.2021.20210034. |
| [24] | JIANG Tao, DANG Yamin, GUO Chunxi, et al. Realization of the international height reference system in the region of Mount Qomolangma[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(8): 1757-1767. DOI: 10.11947/j.AGCS.2022.20210468. |
| [25] | DANG Yamin, JIANG Tao, CHEN Junyong. Review on research progress of the global height datum[J]. Geomatics and Information Science of Wuhan University, 2022, 47(10): 1576-1586. |
| [26] | DANG Yamin, JIANG Tao, GUO Chunxi, et al. Determining the new height of Mount Qomolangma based on the International Height Reference System[J]. Geo-Spatial Information Science, 2023: 1-10. |
| [27] |
WU Fumei, ZENG Anmin, MING Feng. Analyzing the long-term changes in China’s national height datum[J]. Advances in Space Research, 2020, 66(6): 1342-1350.
doi: 10.1016/j.asr.2020.05.027 |
| [28] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008)[J]. Journal of Geophysical Research: Solid Earth, 2012, 117(B4): B04406. |
| [29] | FÖRSTE C, BRUINSMA S, ABRIKOSOV O, et al. EIGEN-6C4—the latest combined global gravity field model including GOCE data up to degree and order 1949 of GFZ Potsdam and GRGS Toulouse[C]// Proceeding of Geophysical Research Abstracts. [S.l.]:EGU, 2014. |
| [30] | LI Jiancheng, CHU Yonghai, XU Xinyu. Determination of vertical datum offset between the regional and the global height datum[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1262-1273. DOI: 10.11947/j.AGCS.2017.20170538. |
| [31] | HE Lin, CHU Yonghai, XU Xinyu, et al. Evaluation of the GRACE/GOCE global geopotential model on estimation of the geopotential value for the China vertical datum of 1985[J]. Chinese Journal of Geophysics, 2019, 62(6): 2016-2026. |
| [32] | LIANG Wei, XU Xinyu, LI Jiancheng, et al. The determination of an ultra-high gravity field model SGG-UGM-1 by combining EGM2008 gravity anomaly and GOCE observation data[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(4): 425-434. DOI: 10.11947/j.AGCS.2018.20170269. |
| [33] | NIE Jianliang, LIU Xiaoyun, TIAN Jie, et al. Vertical movement in Shandong Province based on adaptively dynamic adjustment for level network[J]. Geomatics and Information Science of Wuhan University, 2020, 45(4): 620-625. |
| [34] | DING Alu, TIAN Jie, NIE Jianliang, et al. The adaptive combination adjustment of GNSS and leveling data[J]. Bulletin of Surveying and Mapping, 2019(11): 126-129. DOI: 10.13474/j.cnki.11-2246.2019.0365. |
| [35] | GUO Chunxi, NIE Jianliang, TIAN Jie, et al. Analysis of vertical deformation with the adaptive fusion of GNSS and leveling elevation variation[J]. Geomatics and Information Science of Wuhan University, 2020, 45(1): 7-12. |
| [36] | GUO Chunxi, GUO Xinwei, NIE Jianliang, et al. Establishment of vertical movement model of Chinese mainland by fusion result of leveling and GNSS[J]. Geomatics and Information Science of Wuhan University, 2023, 48(4): 579-586. |
| [37] | WANG Wenli, GUO Chunxi, DING Li, et al. Elevation change analysis of the national first order leveling points in recent 20 years[J]. Acta Geodaetica et Cartographica Sinica, 2019, 48(1): 1-8. DOI: 10.11947/j.AGCS.2019.20170589. |
| [38] | GUO Xinwei, GUO Chunxi, NIE Jianliang, et al. Vertical movement model in Chinese mainland based on first order leveling results[J]. Geomatics and Information Science of Wuhan University, 2022, 47(3): 361-368. |
| [39] | FU Yanguang, FENG Yikai, ZHOU Dongxu, et al. Accuracy assessment of global ocean tide models in the South China Sea using satellite altimeter and tide gauge data[J]. Acta Oceanologica Sinica, 2020, 39(12): 1-10. |
| [40] | ZHOU Dongxu, SUN Weikang, FU Haide, et al. Accuracy assessment of three latest global ocean tide models in coastal areas of China[J]. Advances in Marine Science, 2023, 41(1): 54-63. |
| [41] |
LI Jie, FU Yanguang, TANG Qiuhua, et al. Accuracy assessment of a seamless depth datum model established on the basis of the global ocean tide model[J]. Journal of Coastal Research, 2020, 99(S1): 74-78.
doi: 10.2112/SI99-011.1 |
| [42] | FENG Yikai, YANG Long, FU Yanguang, et al. Accuracy evaluation of the coastal vertical datum transformation model in Shandong Province[J]. Advances in Marine Science, 2023, 41(3): 488-497. |
| [43] |
KE Hao, LI Fei, AI Songtao, et al. Establishment of chart datum and vertical datum transformation for hydrography in the Chinese Great Wall Bay, Antarctic Peninsula[J]. Journal of Surveying Engineering, 2020, 146(2): 05020003.
doi: 10.1061/(ASCE)SU.1943-5428.0000312 |
| [44] | WEI Ziqing. Introduction to the second geodetic boundary value problem[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(6): 797-803. DOI: 10.11947/j.AGCS.2022.20220067. |
| [45] | Shen Wenbin, Sun Xiao, Cai Chenghui, et al. Geopotential determination based on a direct clock comparison using two-way satellite time and frequency transfer[J]. TAO: Terrestrial, Atmospheric and Oceanic Sciences, 2019, 30(1): 2. |
| [46] | LI XinXing, LI JianCheng, LIU XiaoGang, et al. Spherical harmonic synthesis of local hexagonal grid point gravity anomalies with non-full-order Legendre method combined with spherical harmonic rotation transformation[J]. Chinese Journal of Geophysics, 2021, 64(11): 3933-3947. |
| [47] |
LI XinXing, LI JianCheng, Tong Xiaohua, et al. The employment of quasi-hexagonal grids in spherical harmonic analysis and synthesis for the earth’s gravity field[J]. Journal of Geodesy, 2022, 96(11): 89.
doi: 10.1007/s00190-022-01653-6 |
| [48] |
YANG Meng, HIRT C, WU Bin, et al. Residual terrain modelling: the harmonic correction for geoid heights[J]. Surveys in Geophysics, 2022, 43(4): 1201-1231.
doi: 10.1007/s10712-022-09694-4 |
| [49] |
SUN Rong. New algorithms for spherical harmonic analysis of area mean values over blocks delineated by equiangular and Gaussian grids[J]. Journal of Geodesy, 2021, 95(5): 47.
doi: 10.1007/s00190-021-01495-8 |
| [50] | HUANG Motao, CHEN Xin, DENG Kailiang, et al. A general model for compensating remainder dynamic environment effect on marine and airborne gravimetry[J]. Acta Geodaetica et Cartographica Sinica, 2020, 49(2): 135-146. DOI: 10.11947/j.AGCS.2020.20190010. |
| [51] | HUANG Motao, DENG Kailiang, WU Taiqi, et al. A rigorous modification model and its application for computing the vertical gradient of gravity anomaly[J]. Chinese Journal of Geophysics, 2022, 65(12): 4616-4627. |
| [1] | Shuqiang XUE, Tianhe XU, Yanxiong LIU, Anmin ZENG, Baogui KE, Shuang ZHAO. Recent Advances in Marine Geodesy of China [J]. Journal of Geodesy and Geoinformation Science, 2023, 6(3): 58-66. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||